something's got to give

I heard a radio news report this morning again telling the public not to worry, that there is plenty of energy in various forms “at the current rate of consumption”.

“…at the current rate of consumption, the coal reserve will indeed last roughly 250 years.”
- Physics Today Online

“The current estimate of the natural gas resource base in the 48 states…is equivalent to at least 65 to 70 years of supply at the current level of consumption…”
- American Gas Association

“How much uranium is there? The present reserves and resources… are about 3.5 million tones. This is enough to last some fifty years at the current consumption rate.”
-Open Democracy . Net

But something occurred to me. Isn’t our current financial system based on compounding interest? Isn’t the United States economy and by default the world economy based on growth?

“Since 1970, [United States] GDP growth has averaged 3.16 percent per year, after inflation.”
- The Heritage Foundation

“Between 1970 and 1995, a period of slow growth compared with the post-war decades, the Gross World Product grew by 2.9 percent annually” (Figure 1)
- The End of Economic Growth by Charles Siegel

Graph by: Organisation for Economic Co-operation and Development


Isn’t our population in this country and on this planet increasing? Won’t these additional persons want to drive and to eat and stay warm in the winter?


“…the total world demand for energy has increased by 32% between 1980 and 1998.
During the same period, the population increased by 33%.”
- Energy Information Administration

Graph by: Physics Today October 2005

How can we be so blind as to accept predictions of ample energy “at the current rate of consumption” and still expect population growth and economic prosperity to continue?

Something’s got to give.

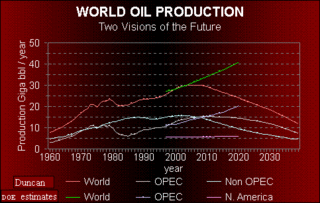Graph from: The Peak of Oil Production and the Road to the Oldvai By Richard C. Duncan

For more on exponential growth you’re welcome to read the following excerpt from "Forgotten Fundamentals of the Energy Crisis" by Dr. Albert A. Bartlett.

When a quantity such as the rate r( t ) of consumption of a resource grows a fixed percent per year, the growth is exponential:
r ( t ) = r0 e k t = r0 2 t / T2

where r0 is the current rate of consumption at t = 0, e is the base of natural logarithms, k is the fractional growth per year, and t is the time in years. The growing quantity will increase to twice its initial size in the doubling time T2where: T2 (yr) = (ln 2) / k » 70 / P

and where P, the percent growth per year, is 100k. The total consumption of a resource between the present (t = 0) and a future time T is:
C = {T to 0} r(t) dt

The consumption in a steady period of growth is:
C = r0 {T to 0} e kt dt = ( r0 / k ) ( e kt - 1 )

If the known size of the resource is R tons, then we can determine the exponential expiration time (EET) by finding the time Te at which the total consumption C is equal to R: R = ( r0 / k ) ( e kTe - 1 )

We may solve this for the exponential expiration time Te where:
EET = Te = ( 1 / k ) ln ( k R / r0 + 1 )

This equation is valid for all positive values of k and for those negative values of k for which the argument of the logarithm is positive.

-Albert A. Bartlett, Professor Emeritus of Physics at the University of Colorado in Boulder